O código deste blog, junto com o conjunto de dados, está disponível no seguinte link https: // github.com / shekharpandey89 / k-means
O cluster K-Means é um algoritmo de aprendizado de máquina não supervisionado. Se compararmos o algoritmo de agrupamento não supervisionado K-Means com o algoritmo supervisionado, não é necessário treinar o modelo com os dados rotulados. O algoritmo K-Means é usado para classificar ou agrupar diferentes objetos com base em seus atributos ou características em um número K de grupos. Aqui, K é um número inteiro. O K-Means calcula a distância (usando a fórmula da distância) e, em seguida, encontra a distância mínima entre os pontos de dados e o cluster de centróide para classificar os dados.
Vamos entender o K-Means usando o pequeno exemplo usando os 4 objetos, e cada objeto tem 2 atributos.
| ObjectsName | Attribute_X | Attribute_Y |
|---|---|---|
| M1 | 1 | 1 |
| M2 | 2 | 1 |
| M3 | 4 | 3 |
| M4 | 5 | 4 |
K-Means para resolver o exemplo numérico:
Para resolver o problema numérico acima por meio de K-médias, temos que seguir as seguintes etapas:
O algoritmo K-Means é muito simples. Primeiro, temos que escolher qualquer número aleatório de K e, em seguida, escolher os centróides ou o centro dos clusters. Para escolher os centróides, podemos escolher qualquer número aleatório de objetos para a inicialização (depende do valor de K).
As etapas básicas do algoritmo K-Means são as seguintes:
- Continua a correr até que nenhum objeto se mova de seus centróides (estável).
- Primeiro, escolhemos alguns centróides aleatoriamente.
- Em seguida, determinamos a distância entre cada objeto e centróides.
- Agrupando os objetos com base na distância mínima.
Portanto, cada objeto tem dois pontos como X e Y, e eles representam no espaço do gráfico da seguinte forma:
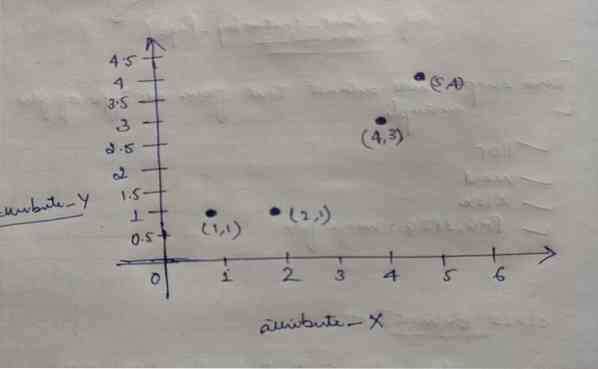
Então, inicialmente escolhemos o valor de K = 2 como aleatório para resolver nosso problema acima.
Etapa 1: inicialmente, escolhemos os dois primeiros objetos (1, 1) e (2, 1) como nossos centróides. O gráfico abaixo está mostrando o mesmo. Chamamos esses centróides de C1 (1, 1) e C2 (2,1). Aqui, podemos dizer que C1 é o grupo_1 e C2 é o grupo_2.
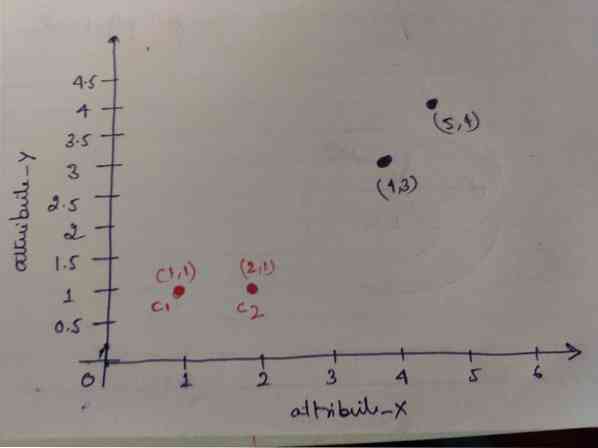
Etapa 2: Agora, calcularemos cada ponto de dados do objeto para centróides usando a fórmula da distância Euclidiana.
Para calcular a distância, usamos a seguinte fórmula.

Calculamos a distância dos objetos aos centróides, conforme mostrado na imagem abaixo.

Então, calculamos a distância de cada ponto de dados do objeto através do método de distância acima, finalmente obtemos a matriz de distância conforme mostrado abaixo:
DM_0 =
| 0 | 1 | 3.61 | 5 | C1 = (1,1) cluster1 | grupo 1 |
| 1 | 0 | 2.83 | 4.24 | C2 = (2,1) cluster2 | grupo_2 |
| UMA | B | C | D | |
|---|---|---|---|---|
| 1 | 2 | 4 | 5 | X |
| 1 | 1 | 3 | 4 | Y |
Agora, calculamos o valor da distância de cada objeto para cada centróide. Por exemplo, os pontos do objeto (1,1) têm um valor de distância para c1 é 0 e c2 é 1.
Como, a partir da matriz de distância acima, descobrimos que o objeto (1, 1) tem uma distância para o cluster1 (c1) é 0 e para o cluster2 (c2) é 1. Então, o objeto um está perto do próprio cluster1.
Da mesma forma, se verificarmos o objeto (4, 3), a distância para o cluster1 é 3.61 e para o cluster2 é 2.83. Então, o objeto (4, 3) mudará para o cluster2.
Da mesma forma, se você verificar o objeto (2, 1), a distância para o cluster1 é 1 e para o cluster2 é 0. Então, este objeto mudará para o cluster2.
Agora, de acordo com seu valor de distância, agrupamos os pontos (agrupamento de objetos).
G_0 =
| UMA | B | C | D | |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | grupo 1 |
| 0 | 1 | 1 | 1 | grupo_2 |
Agora, de acordo com seu valor de distância, agrupamos os pontos (agrupamento de objetos).
E, finalmente, o gráfico ficará como abaixo após fazer o agrupamento (G_0).
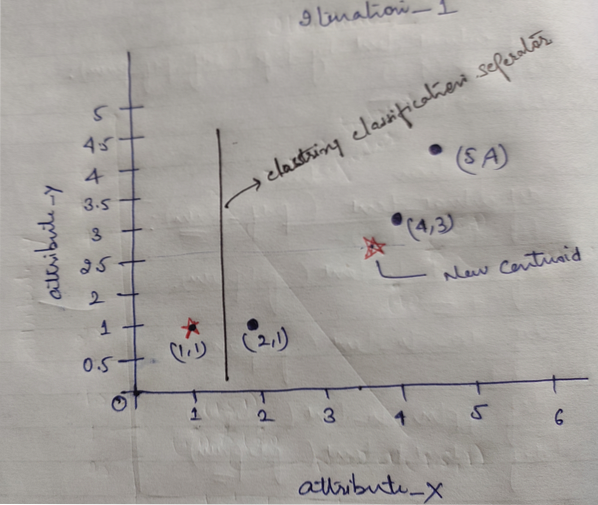
Iteração_1: Agora, vamos calcular novos centróides à medida que os grupos iniciais mudaram por causa da fórmula da distância, conforme mostrado no G_0. Então, o grupo_1 tem apenas um objeto, então seu valor ainda é c1 (1,1), mas o grupo_2 tem 3 objetos, então seu novo valor de centróide é 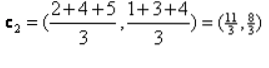
Então, novos c1 (1,1) e c2 (3.66, 2.66)
Agora, novamente temos que calcular toda a distância para os novos centróides como calculamos antes.
DM_1 =
| 0 | 1 | 3.61 | 5 | C1 = (1,1) cluster1 | grupo 1 |
| 3.14 | 2.36 | 0.47 | 1.89 | C2 = (3.66,2.66) cluster2 | grupo_2 |
| UMA | B | C | D | |
|---|---|---|---|---|
| 1 | 2 | 4 | 5 | X |
| 1 | 1 | 3 | 4 | Y |
Iteration_1 (clustering de objetos): Agora, em nome do novo cálculo da matriz de distância (DM_1), nós o agrupamos de acordo com isso. Então, mudamos o objeto M2 do grupo_2 para o grupo_1 como a regra de distância mínima para os centróides, e o resto do objeto será o mesmo. Portanto, o novo agrupamento será como abaixo.
G_1 =
| UMA | B | C | D | |
|---|---|---|---|---|
| 1 | 1 | 0 | 0 | grupo 1 |
| 0 | 0 | 1 | 1 | grupo_2 |
Agora, temos que calcular os novos centróides novamente, pois ambos os objetos têm dois valores.
Então, novos centróides serão 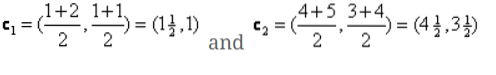
Então, depois de obtermos os novos centróides, o agrupamento ficará assim:
c1 = (1.5, 1)
c2 = (4.5, 3.5)
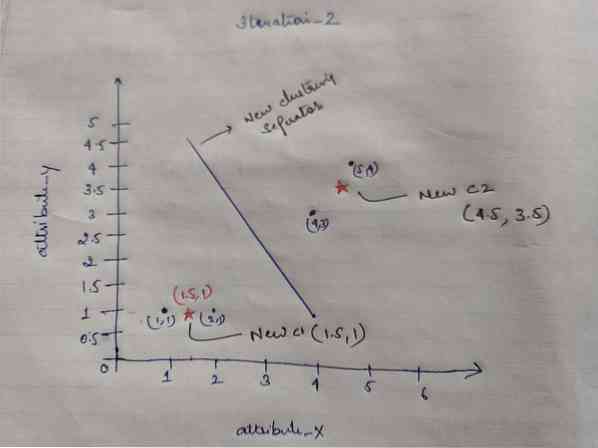
Iteração_2: Repetimos a etapa em que calculamos a nova distância de cada objeto até os novos centróides calculados. Assim, após o cálculo, obteremos a seguinte matriz de distância para iteração_2.
DM_2 =
| 0.5 | 0.5 | 3.20 | 4.61 | C1 = (1.5, 1) cluster1 | grupo 1 |
| 4.30 | 3.54 | 0.71 | 0.71 | C2 = (4.5, 3.5) cluster2 | grupo_2 |
A B C D
| UMA | B | C | D | |
|---|---|---|---|---|
| 1 | 2 | 4 | 5 | X |
| 1 | 1 | 3 | 4 | Y |
Novamente, fazemos as atribuições de agrupamento com base na distância mínima, como fizemos antes. Depois de fazer isso, temos a matriz de agrupamento que é a mesma que G_1.
G_2 =
| UMA | B | C | D | |
|---|---|---|---|---|
| 1 | 1 | 0 | 0 | grupo 1 |
| 0 | 0 | 1 | 1 | grupo_2 |
Como aqui, G_2 == G_1, então nenhuma outra iteração é necessária, e podemos parar aqui.
Implementação de K-Means usando Python:
Agora, vamos implementar o algoritmo K-means em python. Para implementar o K-means, vamos usar o famoso conjunto de dados Iris, que é de código aberto. Este conjunto de dados tem três classes diferentes. Este conjunto de dados tem basicamente quatro recursos: Comprimento da sépala, largura da sépala, comprimento da pétala e largura da pétala. A última coluna indicará o nome da classe dessa linha como setosa.
O conjunto de dados se parece com o seguinte:
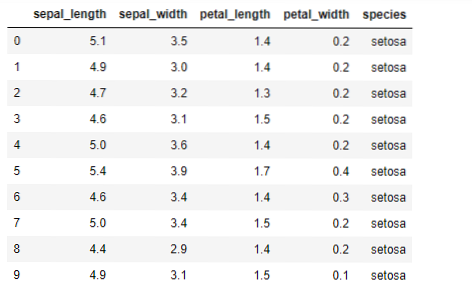
Para a implementação python k-means, precisamos importar as bibliotecas necessárias. Então, importamos Pandas, Numpy, Matplotlib e também KMeans do sklearn.clutser conforme indicado abaixo:

Estamos lendo o Iris.O conjunto de dados csv usando o método read_csv do panda e irá mostrar os 10 melhores resultados usando o método head.
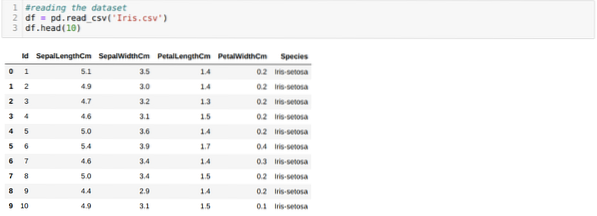
Agora, estamos lendo apenas os recursos do conjunto de dados necessários para treinar o modelo. Portanto, estamos lendo todas as quatro características dos conjuntos de dados (comprimento da sépala, largura da sépala, comprimento da pétala, largura da pétala). Para isso, passamos os quatro valores de índice [0, 1, 2, 3] para a função iloc do quadro de dados do panda (df) como mostrado abaixo:
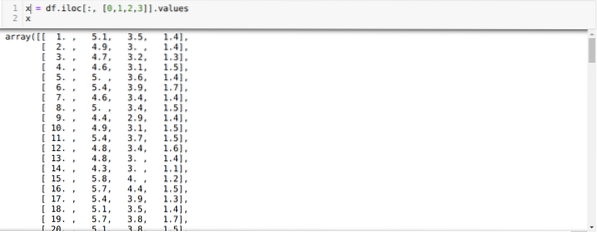
Agora, escolhemos o número de clusters aleatoriamente (K = 5). Criamos o objeto da classe K-means e, em seguida, ajustamos nosso conjunto de dados x nele para treinamento e predição, conforme mostrado abaixo:
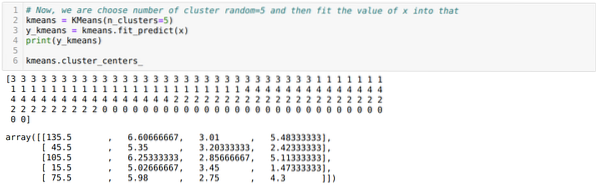
Agora, vamos visualizar nosso modelo com o valor aleatório K = 5. Podemos ver claramente cinco clusters, mas parece que não é preciso, conforme mostrado abaixo.
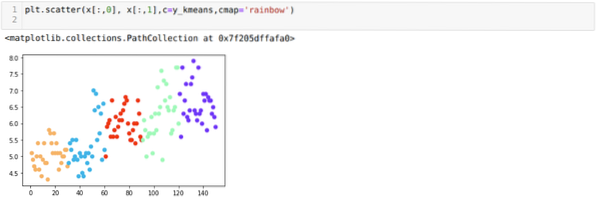
Então, nossa próxima etapa é descobrir se o número de clusters estava correto ou não. E para isso, usamos o método do cotovelo. O método Elbow é usado para descobrir o número ideal do cluster para um determinado conjunto de dados. Este método será usado para descobrir se o valor de k = 5 estava correto ou não, pois não estamos obtendo um agrupamento claro. Depois disso, vamos para o gráfico a seguir, que mostra que o valor de K = 5 não está correto porque o valor ideal fica entre 3 ou 4.
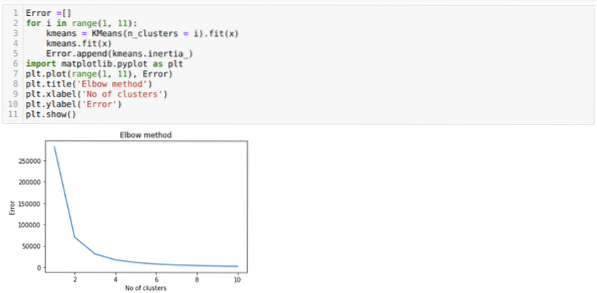
Agora, vamos executar o código acima novamente com o número de clusters K = 4, conforme mostrado abaixo:
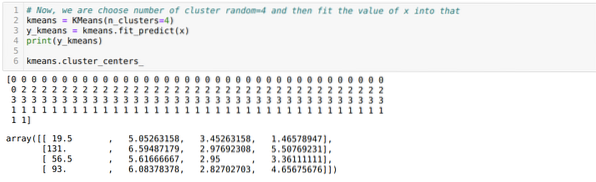
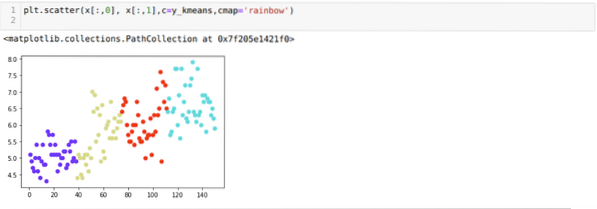
Agora, vamos visualizar o K = 4 agrupamento de novas compilações acima. A tela abaixo mostra que agora o agrupamento é feito através do k-means.
Conclusão
Então, estudamos o algoritmo K-means em código numérico e python. Também vimos como podemos descobrir o número de clusters para um determinado conjunto de dados. Às vezes, o método Elbow não pode fornecer o número correto de clusters, então, nesse caso, existem vários métodos que podemos escolher.
 Phenquestions
Phenquestions


